Young's modulus
In solid mechanics, Young's modulus, also known as the tensile modulus, is a measure of the stiffness of an isotropic elastic material. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds.[1] This can be experimentally determined from the slope of a stress-strain curve created during tensile tests conducted on a sample of the material.
It is also commonly, but incorrectly, called the elastic modulus or modulus of elasticity, because Young's modulus is the most common elastic modulus used, however there are other elastic moduli, such as the bulk modulus and the shear modulus.
Young's modulus is named after Thomas Young, the 19th century British scientist. However, the concept was developed in 1727 by Leonhard Euler, and the first experiments that used the concept of Young's modulus in its current form were performed by the Italian scientist Giordano Riccati in 1782 — predating Young's work by 25 years.[2]
Contents |
Units
Young's modulus is the ratio of stress, which has units of pressure, to strain, which is dimensionless; therefore Young's modulus itself has units of pressure.
The SI unit of modulus of elasticity (E, or less commonly Y) is the pascal (Pa or N/m²); the practical units are megapascals (MPa or N/mm²) or gigapascals (GPa or kN/mm²). In United States customary units, it is expressed as pounds (force) per square inch (psi).
Usage
The Young's modulus allows the behavior of a bar made of an isotropic elastic material to be calculated under tensile or compressive loads. For instance, it can be used to predict the amount a wire will extend under tension or buckle under compression. Some calculations also require the use of other material properties, such as the shear modulus, density, or Poisson's ratio.
Linear versus non-linear
For many materials, Young's modulus is essentially constant over a range of strains. Such materials are called linear, and are said to obey Hooke's law. Examples of linear materials include steel, carbon fiber and glass. Non-linear materials include: rubber and soils (except at very small strains).
Directional materials
Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropic: Their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic, and Young's modulus will change depending on the direction from which the force is applied. Anisotropy can be seen in many composites as well. For example, carbon fiber has a much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood and reinforced concrete. Engineers can use this directional phenomenon to their advantage in creating structures.
Calculation
Young's modulus, E, can be calculated by dividing the tensile stress by the tensile strain:
where
- E is the Young's modulus (modulus of elasticity)
- F is the force applied to the object;
- A0 is the original cross-sectional area through which the force is applied;
- ΔL is the amount by which the length of the object changes;
- L0 is the original length of the object.
Force exerted by stretched or compressed material
The Young's modulus of a material can be used to calculate the force it exerts under a specific strain.
where F is the force exerted by the material when compressed or stretched by ΔL.
Hooke's law can be derived from this formula, which describes the stiffness of an ideal spring:
where
Elastic potential energy
The elastic potential energy stored is given by the integral of this expression with respect to L:
where Ue is the elastic potential energy.
The elastic potential energy per unit volume is given by:
 , where
, where 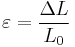 is the strain in the material.
is the strain in the material.
This formula can also be expressed as the integral of Hooke's law:
Relation among elastic constants
For homogeneous isotropic materials simple relations exist between elastic constants (Young's modulus E, shear modulus G, bulk modulus K, and Poisson's ratio ν) that allow calculating them all as long as two are known:
Approximate values

Young's modulus can vary somewhat due to differences in sample composition and test method. The rate of deformation has the greatest impact on the data collected, especially in polymers. The values here are approximate and only meant for relative comparisons.
| Material | GPa | lbf/in² (psi) |
|---|---|---|
| Rubber (small strain) | 0.01-0.1 | 1,500-15,000 |
| ZnO NWs | 21-37 | 3,045,792-5,366,396 |
| PTFE (Teflon) | 0.5 | 75,000 |
| Low density polyethylene | 0.2 | 30,000 |
| HDPE | 0.8 | |
| Polypropylene | 1.5-2 | 217,000-290,000 |
| Bacteriophage capsids[4] | 1-3 | 150,000-435,000 |
| Polyethylene terephthalate | 2-2.7 | |
| Polystyrene | 3-3.5 | 435,000-505,000 |
| Nylon | 2-4 | 290,000-580,000 |
| Diatom frustules (largely silicic acid)[5] | 0.35-2.77 | 50,000-400,000 |
| Medium-density fibreboard[6] | 4 | 580,000 |
| Pine wood (along grain) | 8.963 | 1,300,000 |
| Oak wood (along grain) | 11 | 1,600,000 |
| High-strength concrete (under compression) | 30 | 4,350,000 |
| Magnesium metal (Mg) | 45 | 6,500,000 |
| Aluminium | 69 | 10,000,000 |
| Glass (see chart) | 50-90 | |
| Kevlar[7] | 70.5-112.4 | |
| Mother-of-pearl (nacre, largely calcium carbonate) [8] | 70 | 10,000,000 |
| Tooth enamel (largely calcium phosphate)[9] | 83 | 12,000,000 |
| Brass and bronze | 100-125 | 17,000,000 |
| Titanium (Ti) | 16,000,000 | |
| Titanium alloys | 105-120 | 15,000,000-17,500,000 |
| Copper (Cu) | 117 | 17,000,000 |
| Glass fiber reinforced plastic (70/30 by weight fibre/matrix, unidirectional, along grain) | 40-45 | 5,800,000-6,500,000 |
| Carbon fiber reinforced plastic (50/50 fibre/matrix, unidirectional, along grain) | 125-150 | 18,000,000-22,000,000 |
| Silicon[10] | 185 | |
| Wrought iron | 190–210 | |
| Steel | 200 | 29,000,000 |
| polycrystalline Yttrium iron garnet (YIG)[11] | 193 | 28,000,000 |
| single-crystal Yttrium iron garnet (YIG)[12] | 200 | 30,000,000 |
| Beryllium (Be) | 287 | 42,000,000 |
| Molybdenum (Mo) | 329 | |
| Tungsten (W) | 400-410 | 58,000,000-59,500,000 |
| Sapphire (Al2O3) along C-axis | 435 | 63,000,000 |
| Silicon carbide (SiC) | 450 | 65,000,000 |
| Osmium (Os) | 550 | 79,800,000 |
| Tungsten carbide (WC) | 450-650 | 65,000,000-94,000,000 |
| Single-walled carbon nanotube[13] | 1,000+ | 145,000,000+ |
| Diamond (C)[14] | 1220 | 150,000,000-175,000,000 |
See also
- Deflection
- Deformation
- Elastic Modulus
- Hardness
- Hooke's law
- Shear modulus
- Bending stiffness
- Impulse excitation technique
- Toughness
- Yield (engineering)
- List of materials properties
Notes
- ↑ IUPAC Gold Book internet edition: "modulus of elasticity (Young's modulus), E".
- ↑ The Rational Mechanics of Flexible or Elastic Bodies, 1638-1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
- ↑ http://www.engineeringtoolbox.com/young-modulus-d_417.html
- ↑ Ivanovska IL, de Pablo PJ, Sgalari G, MacKintosh FC, Carrascosa JL, Schmidt CF, Wuite GJL (2004). "Bacteriophage capsids: Tough nanoshells with complex elastic properties". Proc Nat Acad Sci USA. 101 (20): 7600–5. doi:10.1073/pnas.0308198101. PMID 15133147.
- ↑ Subhash G, Yao S, Bellinger B, Gretz MR. (2005). "Investigation of mechanical properties of diatom frustules using nanoindentation". J Nanosci Nanotechnol. 5 (1): 50–6. doi:10.1166/jnn.2005.006. PMID 15762160.
- ↑ Material Properties Data: Medium Density Fiberboard (MDF)
- ↑ DuPont (2001). Kevlar Technical Guide. p. 9.
- ↑ A. P. Jackson,J. F. V. Vincent and R. M. Turner (1988). "The Mechanical Design of Nacre". Proc. R. Soc. Lond. B 234: 415–440. doi:10.1098/rspb.1988.0056. http://rspb.royalsocietypublishing.org/content/234/1277/415.abstract.
- ↑ M. Staines, W. H. Robinson and J. A. A. Hood (1981). "Spherical indentation of tooth enamel". Journal of Materials Science. http://www.springerlink.com/content/w125706571032231/.
- ↑ http://www.ioffe.ru/SVA/NSM/Semicond/Si
- ↑ Chou, H. M.; Case, E. D. (November, 1988). "Characterization of some mechanical properties of polycrystalline yttrium iron garnet (YIG) by non-destructive methods". Journal of Materials Science Letters 7 (11): 1217–1220. doi:10.1007/BF00722341..
- ↑ http://www.isowave.com/pdf/materials/Yttrium_Iron_Garnet.pdf YIG properties
- ↑ "Electronic and mechanical properties of carbon nanotubes". http://ipn2.epfl.ch/CHBU/papers/ourpapers/Forro_NT99.pdf.
- ↑ Spear and Dismukes (1994). Synthetic Diamond - Emerging CVD Science and Technology. Wiley, NY. ISBN 9780471535898.
External links
- Matweb: free database of engineering properties for over 63,000 materials
- Young's Modulus for groups of materials, and their cost
|
|||||
|
|||||
| Conversion formulas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas. | ||||||||||
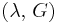 |
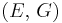 |
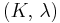 |
 |
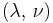 |
 |
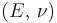 |
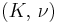 |
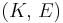 |
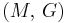 |
|
 |
 |
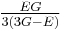 |
 |
 |
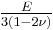 |
 |
||||
 |
 |
 |
 |
 |
 |
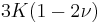 |
 |
|||
 |
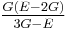 |
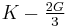 |
 |
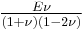 |
 |
 |
 |
|||
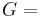 |
 |
 |
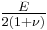 |
 |
 |
|||||
 |
 |
 |
 |
 |
 |
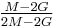 |
||||
 |
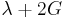 |
 |
 |
 |
 |
 |
 |
 |
 |
|
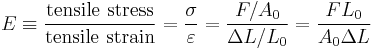
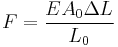
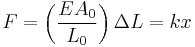

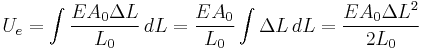
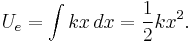
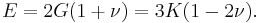
 ) • Young's modulus (
) • Young's modulus ( ) • Lamé's first parameter (
) • Lamé's first parameter ( ) •
) •  ) •
) •  ) • P-wave modulus (
) • P-wave modulus ( )
)